Rise of Kingdoms holiday events come around every few months. The last one involved collecting ornaments for the Christmas tree, and the current Valentine’s Day event requires collection of roses. Using a rose gives you points, and you need a certain number of points to complete the event. We know how many points are needed in total to complete the event (2888 in the case of Valentine’s Day), but the problem is that each rose gives you a varying number of points due to critical hits. For example, using one rose could give you 1 point or it could give you 8 points. So how many roses do you actually need to complete the event? We can get an (approximate) answer to this using probability.
Data Collection
First, we need some data. I used 500 roses and recorded how many points each rose gave. Here you can see the frequency with which a rose gave a certain number of points:
| Points | Frequency |
| 1 | 289 |
| 2 | 131 |
| 3 | 57 |
| 5 | 17 |
| 8 | 6 |
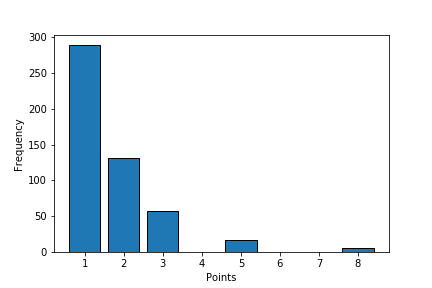
A few things to note. This is a small sample size, so I didn’t see any x4, x6, or x7 critical hits. They might be possible, they might not be. You will get 1 point the majority of the time, and there appears to be an exponential decay in frequency as the point value increases.
Probabilities and Expected Values
Based on the sample data, we can calculate the probability of each point value occurring. To formalize things a bit, let \(X\) be a discrete random variable representing the number of points gained from a single use of a rose. The probability mass function, \(p_X(x)\), can be calculated from the sample by dividing the frequency of each point value by the total number of observations:
\(
p_X(x) = \begin{cases}
\frac{289}{500}, x \in \{1\}, \\
\frac{131}{500}, x \in \{2\}, \\
\frac{57}{500}, x \in \{3\}, \\
\frac{17}{500}, x \in \{5\}, \\
\frac{6}{500}, x \in \{8\}.
\end{cases}
\)
Once we know the mass of \(X\), we can calculate its expected value, \(E[X]\), which tells us the number of points we can expect to receive for each rose:
\(
\begin{align}
\displaystyle E[X] =& \, \sum_{i=1}^{5} x_i P(X = x_i) \\[10pt]
E[X] =& \, (1 \times \frac{289}{500}) + (2 \times \frac{131}{500}) + (3 \times \frac{57}{500}) \,+ \\
& \,(5 \times \frac{17}{500}) + (8 \times \frac{6}{500}) \\[10pt]
E[X] =& \, 1.71
\end{align}
\)
Therefore, we can expect to receive 1.71 points per rose.
How many roses do we need?
Given that we need 2888 points in total, and each rose provides 1.71 points, the total number of roses required is simply \(2888 \div 1.71 = 1688.89\).
Bear in mind that 1) we had a small sample size and 2) we are dealing with probabilities, so there will be some amount of error around that estimate. Regardless, that is a good ballpark estimate of how many roses you should save up to complete the event.
Similar calculations can be done for any of the holiday events, although the probabilities may vary so it would be wise to gather a new sample for each event before calculating the expected value.
If you’re interested, you can find my other Rise of Kingdoms posts here.