Here it is. The answer to the age-old question. The question that shows up at least once a day on Reddit and Discord: “should I save my gold keys and open them all at once?”. The assumption being that opening gold keys together in a batch gives more/better rewards than opening them one at a time. Therefore, in this post we will test whether that is true.
As always, you can find the code and dataset for this analysis in my GitHub repo here.
Samples and expected distributions
We’ll begin with a quick primer on expected/population distributions and how they relate to samples. I’ll try to keep this as short and intuitive as possible, however, it’s an important concept to understand for interpreting the graphs later.
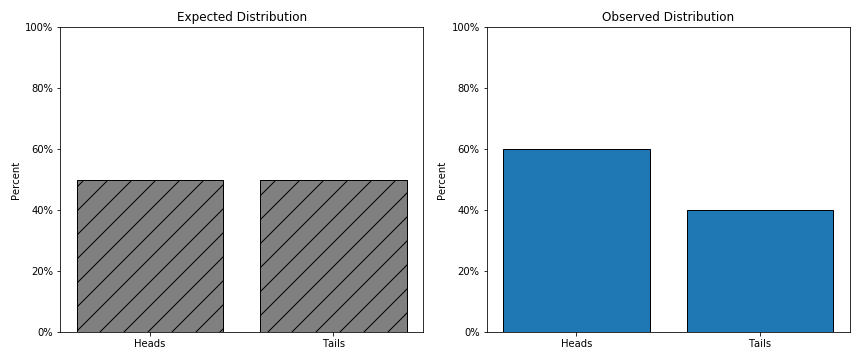
Let’s say we flip a coin an infinite number of times. What proportion of heads and tails would you expect to see? The answer is 50% heads and 50% tails, and would look something like the graph below on the left.
However, we clearly can’t perform infinite coin flips. Instead what we do is take a sample. So lets say we flip a coin 100 times, and see that 60% of the time we land on heads, and 40% of the time we land on tails. The graph above on the right shows our observed sample of coin flips.
Just because in this particular sample we saw 60% heads, intuitively we know that this coin won’t always be 60% heads. If we flipped another 100 times the proportions may be completely different. So we have this intuition that there is always some amount of error whenever we take a sample of something.
When looking at a sample distribution like the one above, it is tempting to say that the coin is biased towards heads just because the heads bar is larger than the tails bar. The key point I want to get across is that we should avoid that temptation. Just because it looks larger in one sample, doesn’t mean that is generally true in the overall population.
What does this have to do with the game?
To put this into the context of Rise of Kingdoms, if you open a gold chest and see 3 legendary sculptures and only 1 resource item, would you conclude that gold chests in general are highly likely to give you sculptures? I’m sure you’ve seen that situation happen, but you would never conclude that you’ll be drowning in legendary sculptures just because you received a lot of them from 1 gold chest. We need a larger sample and to conduct a statistical test that accounts for error in sampling.
This is a very very simplified overview of sampling (apologies to anyone that is already familiar with statistics), but I see incorrect conclusions being drawn all the time. Just because one bar looks larger than another on a graph doesn’t mean that it actually is. The key is to look at the statistical test. Keep this in mind when interpreting the rest of the graphs below.
Saving and using gold keys
The central question is: do you get better rewards by saving gold keys and opening everything at the same time (batch method), or by opening the same number of chests one at a time (single method)?
To test this, I saved 201 gold keys and opened them in batch. Then I saved another 201 gold keys and used them individually. After opening everything, the individual singles method gave me a total of 1297 items, and the batch method gave me a total of 1304 items.
The rewards list (probability section) in the Tavern tells us the expected distribution of items from a gold chest. For example, ‘Legendary Commander Sculpture’ has a probability of 3.023%. My interpretation of this value is that if you look at all of the items you’ll ever receive from gold chests, 3.023% of them will be legendary sculptures. These expected percentage values are plotted below in grey for each reward type.
Additionally, I took every item received from the single method and calculated the proportion (percentage) of the total number of items for each reward type. This is plotted above in blue. The same was done for the batch method and plotted in green.
As an example, let’s look at Epic Commander Sculptures. The Tavern tells us we should expect 7.983% of all chest items to be epic sculptures. After opening chests using the single method, we see that epic sculptures actually make up 17.43% of all chest items. And using the batch method, epic sculptures make up 16.95% of the total.
In general, there is quite a difference between our expected distribution of items (grey) and our sample distributions (blue and green). In some cases we receive more than expected, and in other cases we get a lot less.
Do we meet expectation?
As I stressed in the primer section above, we shouldn’t draw any conclusions from just the height of the individual bars. So let’s take a closer look using statistics.
Single method vs. expectation
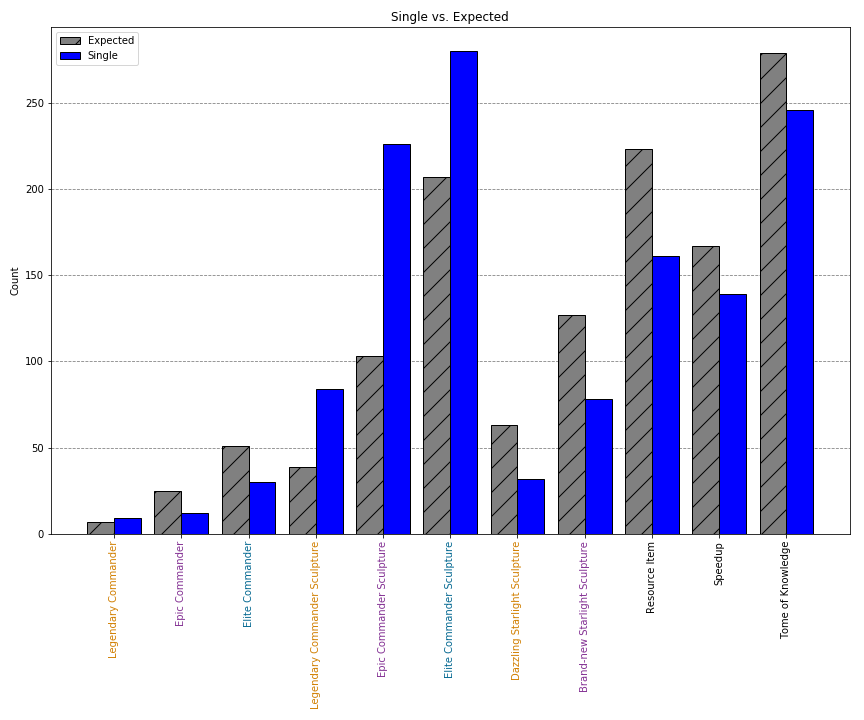
Below you can see the actual number (count) of rewards I received of each type using the single method. Given a total of 1297 items, I also calculated the expected number of rewards using the Tavern probabilities. In other words, how should we expect the rewards to be distributed assuming the Tavern probabilities are true?
| Reward | Count |
| Legendary Commander | 9 |
| Epic Commander | 12 |
| Elite Commander | 30 |
| Legendary Sculpture | 84 |
| Epic Sculpture | 226 |
| Elite Sculpture | 280 |
| Dazzling Starlight | 32 |
| Brand-new Starlight | 78 |
| Resource Item | 161 |
| Speedup | 139 |
| Tome of Knowledge | 246 |
Does our observed sample distribution fit the expected distribution given by the Tavern reward list? To compare these two distributions we can use a chi-squared goodness of fit test. I won’t go into how inferential testing works here, but simply put, the test allows us to determine whether our observed distribution of frequencies differs from an expected distribution.
The chi-squared test shows that there is a statistically significant difference between the frequencies of the two distributions: χ2(9) = 300.52, p < .0001. Interestingly, we can see that the expected probability values given by the Tavern are incorrect and don’t match what we actually receive from the chests. However, the rewards we actually receive are more favorable as we tend to receive more of the things that we typically care about (e.g. sculptures) and less of the more trivial items (e.g. resources). Although this is somewhat subjective as it depends on what type of rewards you value.
Batch method vs. expectation
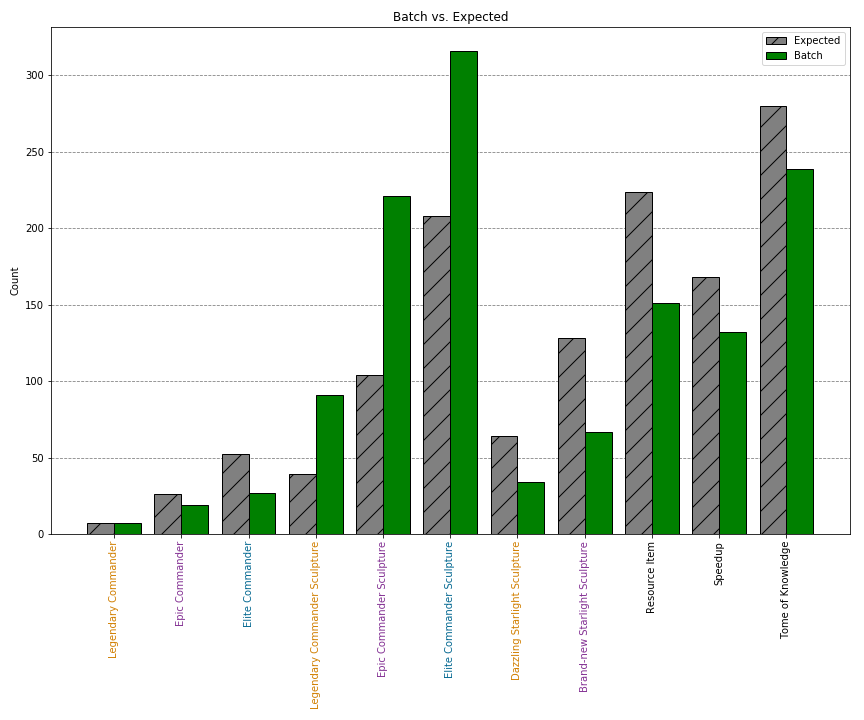
I conducted the same analysis of the items received using the batch method. Below you can see the plot and counts of each reward type, along with the expected distribution assuming 1304 total items.
| Reward | Count |
| Legendary Commander | 7 |
| Epic Commander | 19 |
| Elite Commander | 27 |
| Legendary Sculpture | 91 |
| Epic Sculpture | 221 |
| Elite Sculpture | 316 |
| Dazzling Starlight | 34 |
| Brand-new Starlight | 67 |
| Resource Item | 151 |
| Speedup | 132 |
| Tome of Knowledge | 239 |
Once again, we’ll use a chi-squared goodness of fit test, which shows a statistically significant difference between the frequencies of the two distributions: χ2(9) = 351.58, p < .0001. Like the single method above, the Tavern probabilities don’t match what we actually receive from the gold chests.
An alternate interpretation of Tavern probabilities
While discussing this with Hhobbsy from Everything RoK, he suggested that the probabilities listed in the Tavern may not be referring to percentage of total items received, but rather percentage of the number of instances of items. An instance here is defined as a received reward, ignoring the number of those rewards received.
Chests always have 4 reward instances, but can potentially have more than 4 total items. For example, in the chest below, we received 1 instance of an Epic Commander Sculpture (Sun Tzu), but received a total of 3 epic sculpture items.
In this section, we’ll be counting only instances of rewards, and not the total number of individual items received. For example, ‘Legendary Commander Sculptures’ have a probability of 3.023%. In this alternate interpretation, we take that to mean that a legendary sculpture instance will appear 3.023% of the time, and we ignore how many individual legendary sculpture items we actually received from the chest.
Reanalysis of single method data
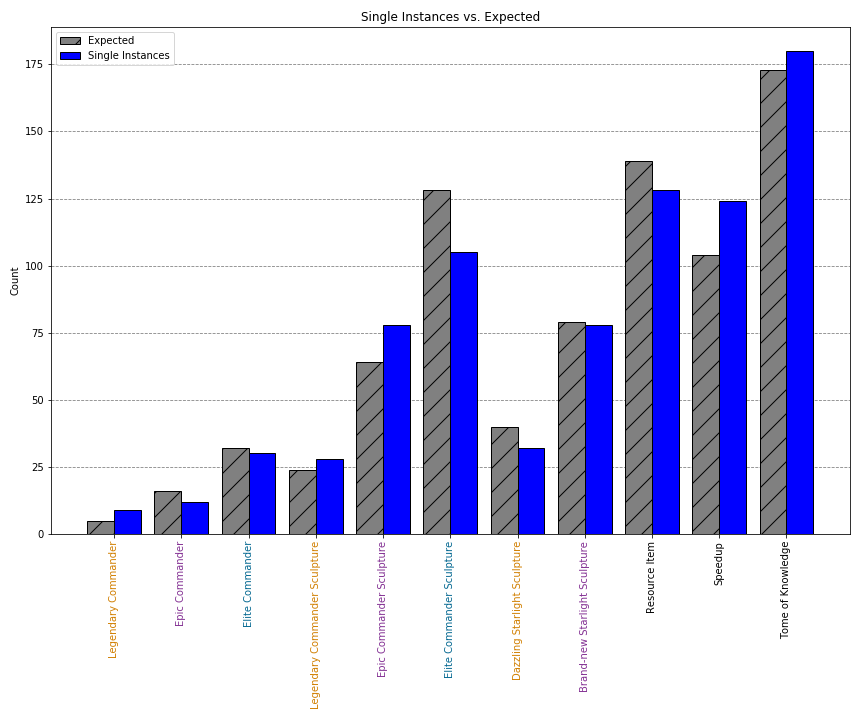
From the single method data we have a total of 201 chests, which equates to 804 reward instances. I re-aggregated the data and counted the number of separate instances of each reward type. I then used the Tavern probabilities to calculate the number of instances we should expect to see for each type of reward. The data is plotted below:
| Reward | Count |
| Legendary Commander | 9 |
| Epic Commander | 12 |
| Elite Commander | 30 |
| Legendary Sculpture | 28 |
| Epic Sculpture | 78 |
| Elite Sculpture | 105 |
| Dazzling Starlight | 32 |
| Brand-new Starlight | 78 |
| Resource Item | 128 |
| Speedup | 124 |
| Tome of Knowledge | 180 |
When we interpret the Tavern probabilities as a probability of all instances, we can see that the reward distribution fits the expected distribution much better. The chi-squared test still indicates that these distributions are different, χ2(9) = 18.80, p = .043, however, the p-value is borderline. While still inconclusive, I think it’s safer to assume that the Tavern probabilities are referring to separate instances of rewards, rather than a probability of the total number of items received.
Should you save your gold keys?
Finally, onto the main event. Is there a difference between the reward distributions using the single method and the batch method?
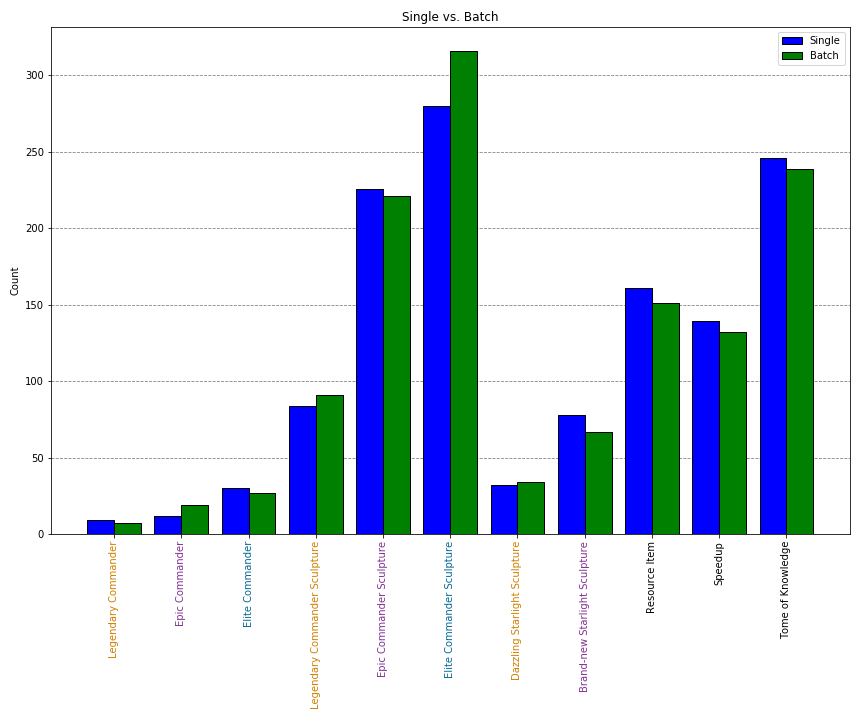
We are now no longer concerned about the expected distribution given by the Tavern. Our goal here is to compare the distributions across our two methods of sampling. Below you’ll see the two distributions plotted on the same graph. This is simply a combination of the observed distributions from the previous two graphs to make things easier to see.
For this analysis we need a slightly different test as we are not comparing against an expected/known distribution, therefore we’ll use the chi-squared test of independence. We have two variables, rewards and method (single/batch), and the test allows us to determine whether these two variables are independent of each other. In other words, does our distribution of rewards depend on which method we used to open the chests?
The chi-squared test retains the null hypothesis in this case, χ2(10) = 5.98, p = .82. Therefore, regardless of which method you use to open the chests, the reward distribution will be the same. Simply put, saving your gold keys and opening chests in batch does nothing for you – you’ll get the same rewards either way.
Notice that the green and blue bars are not exactly equal and that there are slight inconsistencies. At this point, some of you will no doubt look at the graph and say something like “but we get more legendary sculptures and dazzling starlight when we save keys”. No. This is why I started the post with the primer. The data comes from a sample and distributions of samples will always fluctuate. Therefore, you cannot draw conclusions simply by looking at the heights of individual bars.
Summary
There are two conclusions to be drawn here:
- It’s unclear whether the Tavern probabilities refer to total number of items or total number of separate instances. The second interpretation (instances) appears to be a better fit for the data, in which case the Tavern values are a fairly accurate indication of reward probabilities.
- Do you get better rewards by saving your gold keys? Nope.
So, why does everyone think that saving keys leads to better rewards? Where does that assumption come from? My guess is that when you open 200 chests at the same time you’re bombarded with a lot of legendary drops. This feels good and makes it seem like you’re getting a lot good rewards, but is nothing more than a cognitive bias as you’ll receive the same rewards either way.
As always, if you’re interested in my other Rise of Kingdoms posts, you can find them here.