In a previous post I discussed the point requirements of the last holiday event (Valentine’s Day – Pledge of Thorns). Here, I will do the same analysis with the new holiday event (Show Your Love) to confirm those findings. I’ll be drawing comparisons between the two events throughout.
The supporting code and data for this analysis can be found here.
Data collection for event
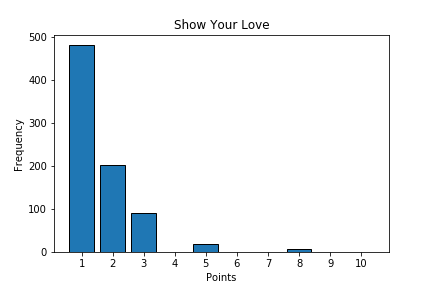
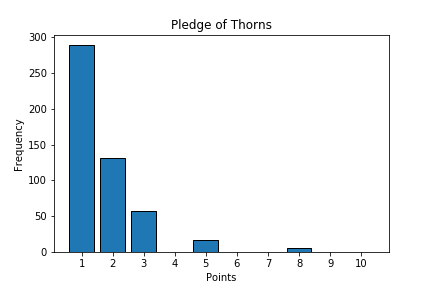
I began by using 800 items (Carnations) and recorded how many points each item provided. Below (left) you can see the frequency distribution of the points provided for each item, as well as the distribution from the previous event (right):
Show Your Love
| Points | Frequency | Proportion |
| 1 | 481 | 0.601 |
| 2 | 202 | 0.253 |
| 3 | 90 | 0.113 |
| 4 | 0 | 0.000 |
| 5 | 19 | 0.024 |
| 6 | 0 | 0.000 |
| 7 | 0 | 0.000 |
| 8 | 8 | 0.010 |
| 9 | 0 | 0.000 |
| 10 | 0 | 0.000 |
Pledge of Thorns
| Points | Frequency | Proportion |
| 1 | 289 | 0.578 |
| 2 | 131 | 0.262 |
| 3 | 57 | 0.114 |
| 4 | 0 | 0.000 |
| 5 | 17 | 0.034 |
| 6 | 0 | 0.000 |
| 7 | 0 | 0.000 |
| 8 | 6 | 0.012 |
| 9 | 0 | 0.000 |
| 10 | 0 | 0.000 |
There are a couple of things to notice here:
- The frequency distribution of points looks extremely similar for the two events, which suggests that the point distribution probabilities have not been changed. This might be a safe assumption moving forward for future events. More on this below.
- A total of 1300 items were used across the two data sets, and
x4,x6,x7,x9, andx10critical hits have not shown up a single time. I think it would be safe to assume these values are not possible in the holiday events.
Event probabilities and expected values
The expected value of a single item is the sum of the point values weighted by their probability of occurrence. I won’t repeat the math here but you can check my previous post for the details. As we derived the probabilities from a sample, the expected value in this case will be equal to the arithmetic mean.
For the current Show Your Love event, the expected value of each item is 1.64. In other words, each Carnation used should give you 1.64 points.
For the previous event, the expected value was 1.71.
How many items do we need?
Like the previous event, this event also requires a total of 2888 points. If each Carnation provides 1.64 points, we will need a total of 1758.30 items.
Notice that this is slightly higher than the 1688.89 required for the previous event. There are a two possible reasons for this:
- If you look at the tables above, you’ll notice that in the current event there is a higher probability of the low value
1xpoints, and a lower probability of the higher value critical hits (e.g.3x,5x,8x). Overall, this reduces the point value per item for this event. This might suggest that the probabilities were changed between the events. - There is a difference in sample size between these two analyses. The current analysis has a larger sample size which results in a more precise estimate.
We can use statistics to rule out the first possibility. The Chi-square and Kolmogorov-Smirnov tests allow us to test for differences between distributions. The results from both tests are as follows:
Chi-square independence test: χ2(4) = 1.68, p = 0.79
Kolmogorov-Smirnov 2 sample test: D = 0.20, p = 0.99
The null hypotheses of the tests are that the two samples are similarly distributed (or that they come from the same distribution) and that point value is independent of the event. We retain the null in both cases, as p > .05, and can say that the probability distributions for both events are essentially the same despite the minor observed differences.
Therefore, we can rule out option #1 as a possibility. Instead, the larger sample size used for this event analysis resulted in a more precise estimate of the expected value, and thus the number of items required.
Summing up…
- You’ll need around 1760 items to complete holiday events (assuming a total requirement of 2888 points)
- The item probabilities don’t appear to change between holiday events
- Only
x1,x2,x3,x5, andx8critical hits are possible
If you’re interested, you can find my other Rise of Kingdoms posts here.